ANALIZA STATYSTYCZNA

SigmaPlot stanowi łatwe w użyciu narzędzie do kompletnej analizy danych i tworzenia wykresów. Funkcjonalność statystyczna została zaprojektowana z myślą o użytkownikach nie będących specjalistami w tej dziedzinie. Ten oparty na kreatorze pakiet oprogramowania statystycznego prowadzi użytkowników przez wszystkie kroki i wykonuje zaawansowaną analizę statystyczną bez konieczności posiadania gruntownej wiedzy z dziedziny statystyki. Każda analiza statystyczna ma pewne założenia, które muszą być spełnione przez zbiór danych. Jeśli wstępne założenia nie są spełnione, można otrzymać błędne lub niewłaściwe wyniki nie wiedząc o tym. Jednak SigmaPlot automatycznie sprawdza, czy zbiór danych spełnia kryteria testowe, a jeśli nie to zaproponuje, który test uruchomić.


Opis danych
Pojedyncza grupa
  • Test - t dla 1 próby
  • Test kolejności par

    • Porównanie dwóch grup
  • Test -t
  • test kolejności par

    • Porównanie wielu grup
  • jednoczynnikowa ANOVA
  • dwuczynnikowa ANOVA
  • trzyczynnikowa ANOVA
  • wieloczynnikowa ANOVA dla czynników wewnątrzgrupowych

    • Przed i po
  • t-test dla par obserwacji
  • test kolejności

    • Powtarzane pomiary
  • jednoczynnikowa ANOVA powtarzanych pomiarów
  • dwuczynnikowa ANOVA powtarzanych pomiarów
  • wieloczynnikowa ANOVA powtarzanych pomiarów

    • Wskazniki i proporcje
  • z-test
  • Chi – kwadrat
  • Test Fisher’a
  • Test McNemars’a
  • Ryzyko Względne
  • iloraz szans

    • Regresje
  • Liniowa
  • Wielokrotna logistyczna
  • Wielomianowa
  • Krokowa
  • Najlepszych podzbiorów
  • Kreator regresji
  • Regresja Deminga
  • Regresja Passing-Bablok
  • Akaike Information Criterion (AICc)

    • Korelacja
  • Współczynnik korelacji Pearson’a,
  • Współczynnik korelacji Spearman’a

    • Analiza Przeżycia
  • Estymator Kaplana-Meiera,
  • Regresja Cox’a

    • Nowe Makra
  • Porównanie wykresu i statystyki z rozkładem normalnym dla wstępnej analizy rozkładu jakości,
  • Analiza linii równoległych w celu określenia czy współczynniki kierunkowe i punkty przecięcia regresji liniowej z osią są różne,
  • Wykres i statystyka Bland-Altman’a jako metody porównawcze
  • One-Way Frequency Tables Method

    Rozszerzenia do istniejących własności
  • Dokładniejsze błędy statystyczne w raportach nieliniowej regresji dla dopasowanych modeli z ograniczeniem rówości
  • Wartości P dodane do wielokrotnych procedur porównawczych Dunnetta i Duncana
  • Poprawa dokładności w wielu statystykach porównawczych dla lepszych efektów w raportach trójskładnikowej analizy wariancji ANOVA

    • Test-t jednej próby

    Test-t jednej próby testuje hipotezę, że mediana populacji równa jest określonej wartości.

    Opis własności – oferowany przez SigmaPlot t-test jednej próby wykorzystuje pojedynczą grupę danych z próby do testowania hipotezy zerowej, że średnia populacji ma określoną wartość. Wartość hipotetycznej średniej jest określony w oknie dialogowym „Test Options”.

    Wniosek z tego, że t-test par jest najprostsze narzędzie dla powtarzalnych pomiarów. W przedstawionym t-teście par różnica pomiędzy pomiarami dwóch grup jest obliczana dla każdego obiektu. Różnice te tworzą pojedynczą grupę, która jest analizowana przy pomocy t-testu jednej próby czy są one próbą z populacji o średniej zerowej.

    Jedynym założeniem przy użyciu t-testu jednej próby jest to, aby próba populacji posiadała rozkład normalny. Mimo, że test ten jest znany jako całkiem silny, może jednak wprowadzać w błąd jeżeli to założenie nie jest spełnione. To prowadzi nas do nieparametrycznej wersji t-testu jednej próby.


    Metoda obliczeniowa
    Głównym założeniem jest dostarczenie procedury ważnej w szerokim zakresie rozkładów do testowania wartości pomiarów głównej tendencji populacji. W tym celu raczej mediana populacji niż średnia jest wartością, którą będziemy testować ponieważ jest odporniejsza na błędy próby. Tak więc korzystając z naszych prób danych chcemy przetestować hipotezę zerową, że mediana populacji jest równa jakiejś określonej wartości. Test zaprojektowany do tego celu jest (dwustronnym) testem par Wilcox’a. Używamy wersji dla dwóch prób dla naszego nieparametrycznego t-testu par, a wersja dla jednej próby może być wprowadzona w podobny sposób. Podstawowym założeniem do użycia tego testu jest aby rozkład populacji bazowej był symetryczny względem mediany.


    Regresja Deminga

    Regresja Deming’a estymuje prawdziwą zależność liniową pomiędzy dwiema zmiennymi, gdzie obserwacje dla obu zmiennych posiadają błędy pomiarowe. Stała wartość błędu może być określona dla każdej zmiennej lub różne wartości błędu mogą być przypisane do każdej obserwacji.



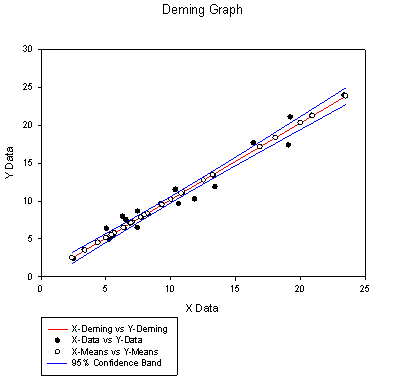
    Opis własności
    Regresja Deminga jest specjalnym przypadkiem regresji błędów w zmiennych (Errors-in-Variables) zwanej również regresją Typu II lub modelem regresji losowej) . Problemem jest określenie najlepszej linii prostej dopasowanej do par obserwacji , w której każda współrzędna posiada błąd pomiaru z jego rzeczywistej wartości. Obliczony współczynnik kierunkowy i punkt przecięcia prostej z osią współrzędnych dla prostych dopasowanych są estymatorami wartości parametrów, które definiują linie odpowiadającą prawdziwym wartościom współrzędnych.

    Pewne założenia są wymagane do otrzymania rozwiązania metodą regresji Deminga. Zakłada się, że pomiary dla obu współrzędnych posiadają dwuwymiarowy rozkład normalny z odchyleniem standardowym populacji, które zostało określone (co najmniej do wielokrotności pewnej stałej wartości) przez użytkownika. Przyjmuje się, że wszystkie pary obserwacji są wybrane niezależnie a dwie współrzędne dla każdej obserwacji są również z założenia niezależne.

    Z powyższych założeń wynika, że maksymalne osiągane prawdopodobieństwo może być użyte do sformułowania problemu Regresji Deminga jako problemu optymalizacji. Dane wejściowe dla regresji Deminga składają się z par obserwacji , gdzie pierwsza współrzędna odnosi się do niezależnej zmiennej a druga do zmiennej zależnej. Błędy danych dla każdej zmiennej wyrażane jako estymacja odchyleń standardowych obserwacj, muszą być również dostarczane przez użytkowników. Głównym celem Regresji Deminga jest określenie współczynnika kierunkowego i punktu przecięcia z osią współrzędnych dla najlepiej dopasowanej prostej.

    Przykłady zastosowania

    1. Badania porównawcze metod w chemii klinicznej.
    2. Uzyskiwanie wykresów izochronu w geochronologii. Jest to uniwersalna metoda datowania skał, osadów i skamieniałości. Wykres jest linią prostą zależności dwóch współczynników izotopów znajdujących się w kilku próbkach mineralnych pochodzących ze wspólnego źródła.
    3. Uzyskanie liniowej zależności między mętnością i zawiesiną stałych stosowanych w ocenie jakości wody.

    Regresja Passing-Bablok
    Regresja Passing-Bablok to transformacja, która stanowi uzupełnienie Regresji Deminga. W ramach wyników transformacja generuje dane wykresów, które mogą być używane do tworzenia następujących typów wykresów, przedstawionych poniżej.